Loop elimination algorithms are commonly used in optimization and graph algorithms to improve performance by removing redundant or unnecessary loops in computations. While the specific use cases may vary, the famous examples where loop elimination algorithms are required are page ranking algorithms, matrix multiplication, compiler optimization and others.

Photo by 愚木混株 cdd20 on Unsplash

My use case is rather different.

I had the chance to travel to southern Spain this year and enjoy my favorite hobby: road biking.

I went there with a few friends and we agreed at the very beginning that we are going to record and share all expenses.

Multiple mobile applications have such functionality. We picked Tricount. It is an easy-to-use application that keeps track of the expenses, shows the balances and at the end of the trip offers a money distribution method.

I had implemented similar software before so I explained how this part of the software works to my friends during one of those long rides in the mountains.

Since it is an interesting topic I will try to do the same for you dear reader …

I will use a group of imaginary friends who went on a trip and decided to share the expenses. Anybody can pay for anything, but they agreed that they will record every spending and then split the expenses equally at the end just as we did.

As with many other things, this problem can be represented by a graph:

Such a graph should have a vertex for each friend in the group. A directed edge is representing a payment obligation.

If there is an outward edge from a vertex then the friend in the starting vertex owes the friend in the ending vertex.

The value is represented by the weight of the edge.

Here is an example of such a graph:

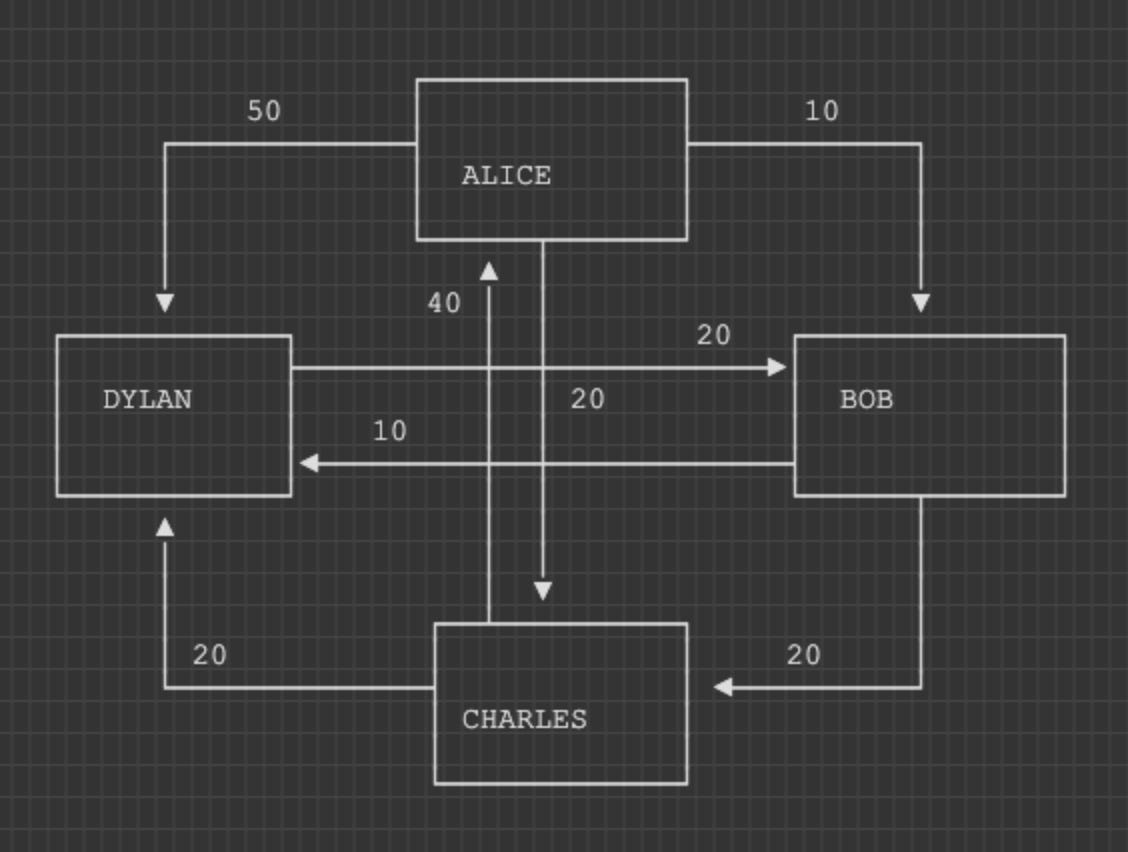
Payment obligations are represented by a graph. Image by the author.

Let us summarise the balances for each friend (the first number is how much each person owes and the second is how much he/she is owed):

Alice: (-80+40) = -40

Bob: (-30+30) = 0

Charles: (-60+40) = -20

Dylan: (-20+80) = 60

If the balance is negative then the person in question should pay the others (he/she paid less than the others during the trip). If the balance is positive then the specific person paid more than the others during the trip.

Since the friends agreed to split the expenses equally the total balance should be always 0.

Our objective is to minimize the number of payments and the amounts thereof that participants need to make after the journey.

This is where loop elimination comes into the picture.

In our example graph, we can easily identify a couple of loops ourselves.

Let us start with a straightforward one: Alice owes Charles 20, while Charles owes Alice 40.

This loop can be eliminated if we deduct what Alice owes to Charles (20) from the amount that Charles should pay to Alice (40).

By executing this step, we effectively eliminate one loop, resulting in Alice not owing anything to Charles, and Charles only having to pay Alice 20 instead of 40.

Now as we understand how loop elimination works we will automate this process by creating an algorithm that can do the above steps even in much bigger graphs.

We will represent our graph using a basic array. The start vertex will be stored at the first index, the end vertex at the second index, and the corresponding value will indicate the amount owed from the first person to the other.

So in our example, the relevant part of our graph will look like this:

$graph['alice']['charles'] = 20;
$graph['charles']['alice'] = 40;

Let us see the core of our code:

public function reducePayments(): self 
{

        // Get the first vertex in the graph
        $vertices = array_keys($this->graph);
        $firstVertex = reset($vertices);

        // Loop until there are no more cycles in the graph
        while ($cycle = $this->findCycle($firstVertex)) {
            // Cancel the cycle
            $this->cancelCycle($cycle);
        }

        return $this;

}

What are we doing here?

We try to find all cycles in our graph and eliminate them one by one.

Our findCycle method is executing a Depth First Search on our graph. I’m not going to detail how DFS works but if you are interested then you can find a link to the full source code at the end of this article.

After identifying a cycle, we must nullify it by decreasing the weight of the edges by the lowest weight in the loop, following the same approach demonstrated in the previous example.

protected function cancelCycle($cycle) 
{

     // Find the minimum weight of the cycle
     $min_weight = $this->minWeight($cycle);

     // Loop through the edges in the cycle
     foreach ($cycle as list($v, $u)) {
         // Subtract the minimum weight from the edge weight
         $this->graph[$u][$v] -= $min_weight;
     }

 }

This method finds the edge with the lowest weight in the cycle and deduces it from all the edges of that cycle.

If the weight of any edge becomes 0 then we are no longer considering it an edge (and it will NOT be used in our DFS search again):

protected function getAdjacentEdges($v) {
    return array_keys(
        // Do not return those edges which are already reduced to 0 weight ...
        array_filter($this->graph[$v], fn($w) => $w !== 0)
    );
}

If we execute our reducePayments method then we will get the following new graph:

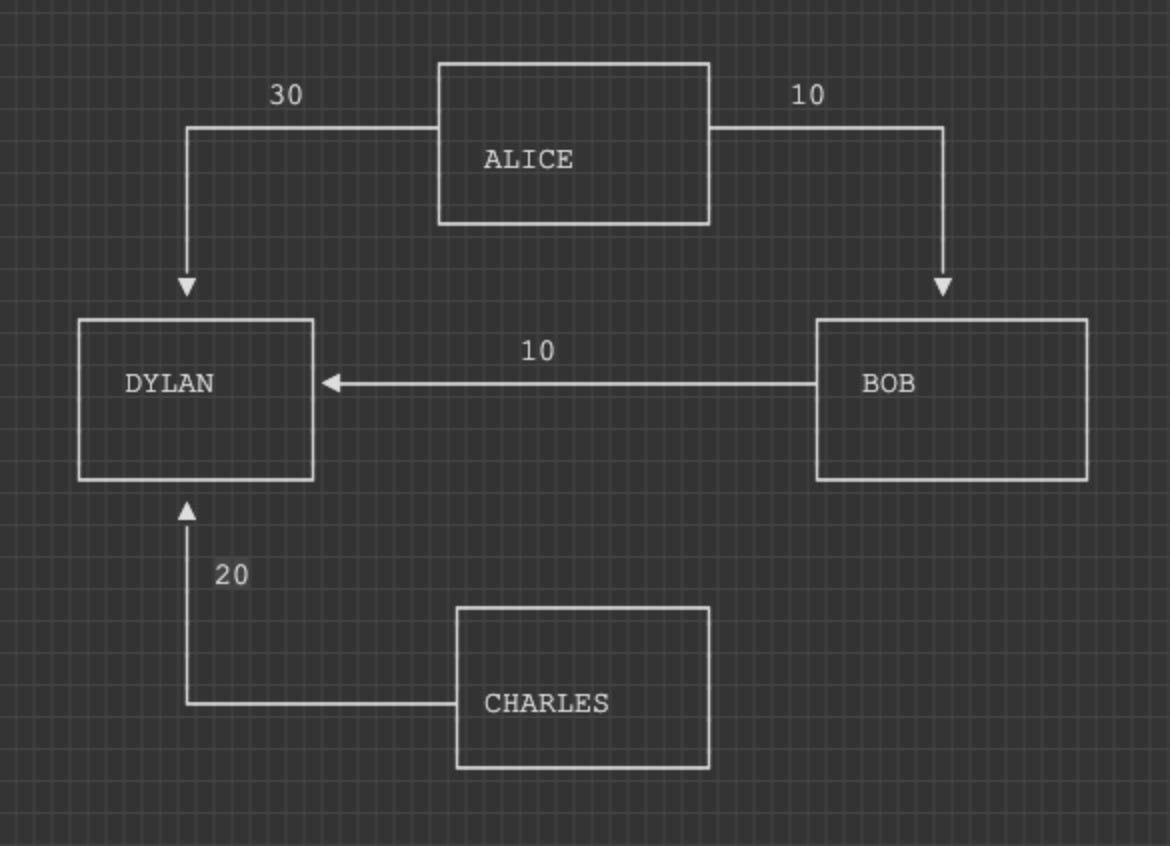
Graph with no loops. Image by the author

You can easily tell that this graph does not have any loops in it.

Let us quickly calculate the balances again:

Alice: (-40+0) = -40

Bob: (-10+10) = 0

Charles: (-20+0) = -20

Dylan: (0+60) = 60

As you can see the balances did not change but the number of payment transactions dropped significantly (from 8 to 4).

This is what we expected.

I hope that now you can explain loop elimination to your friends as well during long rides on the road.

The full source code can be downloaded from here: https://gist.github.com/dihjital/e4353725a27dbbe12da402d771467883