Non-functional requirements are often forgotten aspects of code development.
One of the most well-known non-functional requirements is application performance.
If your application is dealing with a large number of users then this can be translated to various things, typically front-end response time.
Today, it’s no longer a cliché that your competition is just one click away on the Internet.
Photo by Melyna Valle on Unsplash
A couple of months back I had to re-write one of my old applications using Laravel and Livewire.
The application is used to document the cabling layout in a data center. One key feature is the listing of the routes between the connectivity devices. For this purpose, the software uses graph search algorithms, which can explore the paths between the devices and print all the cables along the paths.
Originally I used a BFS-based approach that was quick enough and worked well in an unweighted and undirected graph.
I wanted to explore other approaches, such as incorporating weights into the pathfinding functionality of the application and testing various alternatives to BFS.
In my previous article, I wrote about an algorithm I have developed to find the shortest path between two nodes in a weighted graph. I used Dijkstra’s algorithm with my priority queue to accomplish this.
I also come up with a bidirectional search algorithm based on ChatGPT-generated pseudo-code. ChatGPT provided its version in Python so I had to rewrite the code to PHP but this was much simpler than I thought.
PHP rocks again …. please contact me if you are interested in the final code of bidirectional search in PHP.
After obtaining all three algorithms for comparison, I needed to select a tool that could assist me in comparing their performance.
An obvious choice was phpbench since it is relatively simple to use and in many aspects, it is similar to phpunit.
As the phpbench documentation states:
“PHPBench is a benchmark runner for PHP analogous to PHPUnit but for performance rather than correctness”.
After installing phpbench in my project I created a class file that contains my performance test cases:
/**
* @BeforeMethods({"setUp"})
*/
class GraphTraversalBench
{
private array $fullGraph = [];
private int $start, $end;
private $app;
protected function initializeGraph(): array { ... }
public function setUp() {
...
$this->fullGraph = $this->initializeGraph();
// Select start and end device randomly ...
$this->start = array_rand($this->fullGraph);
do {
$this->end = array_rand($this->fullGraph);
} while ($this->end === $this->start);
}
public function benchBFS()
{
(new Graph(graph: $this->fullGraph))->breadthFirstSearch($this->start, $this->end);
}
public function benchDijkstraWithPriorityQueue()
{
(new Graph(graph: $this->fullGraph))->dijkstraWithPriorityQueue($this->start, $this->end);
}
public function benchBidirectionalSearch()
{
(new Graph(graph: $this->fullGraph))->bidirectionalSearch($this->start, $this->end);
}
}
The code is straightforward:
first, we set up all the class variables so all test methods can use the same graph (fullGraph) with the same start and end nodes,
then we create a new instance of our Graph and call each search method one by one.
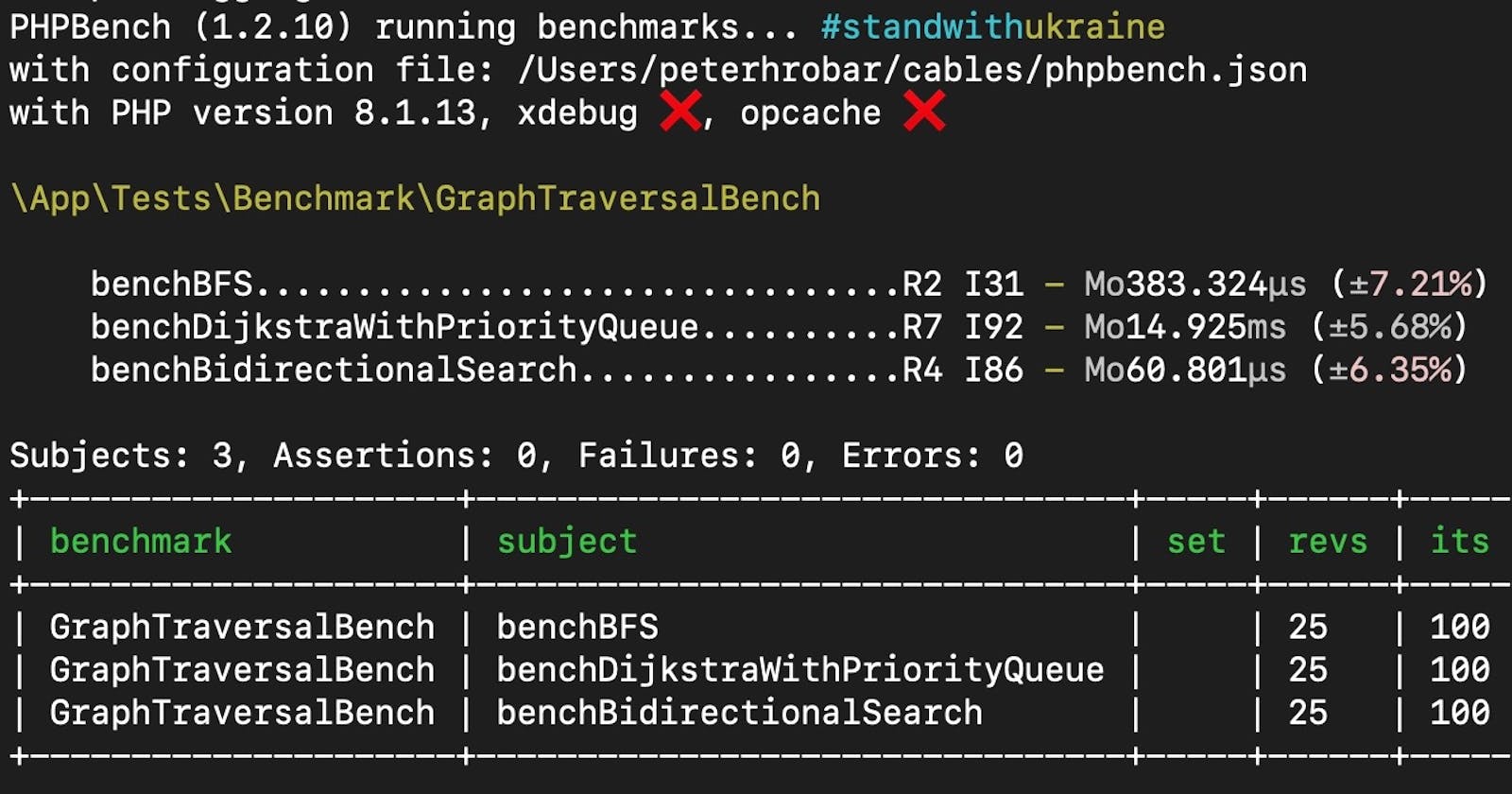
When we run our tests we specify the number of revs and iterations on the command line.
Since we pick a random start and end node for our testing we define a relatively high number of revs and a relatively low number of iterations.
As you can see in the figure below we tested 25 pairs of nodes with all 3 algorithms and we run each algorithm a 100 times for the same start and end nodes.
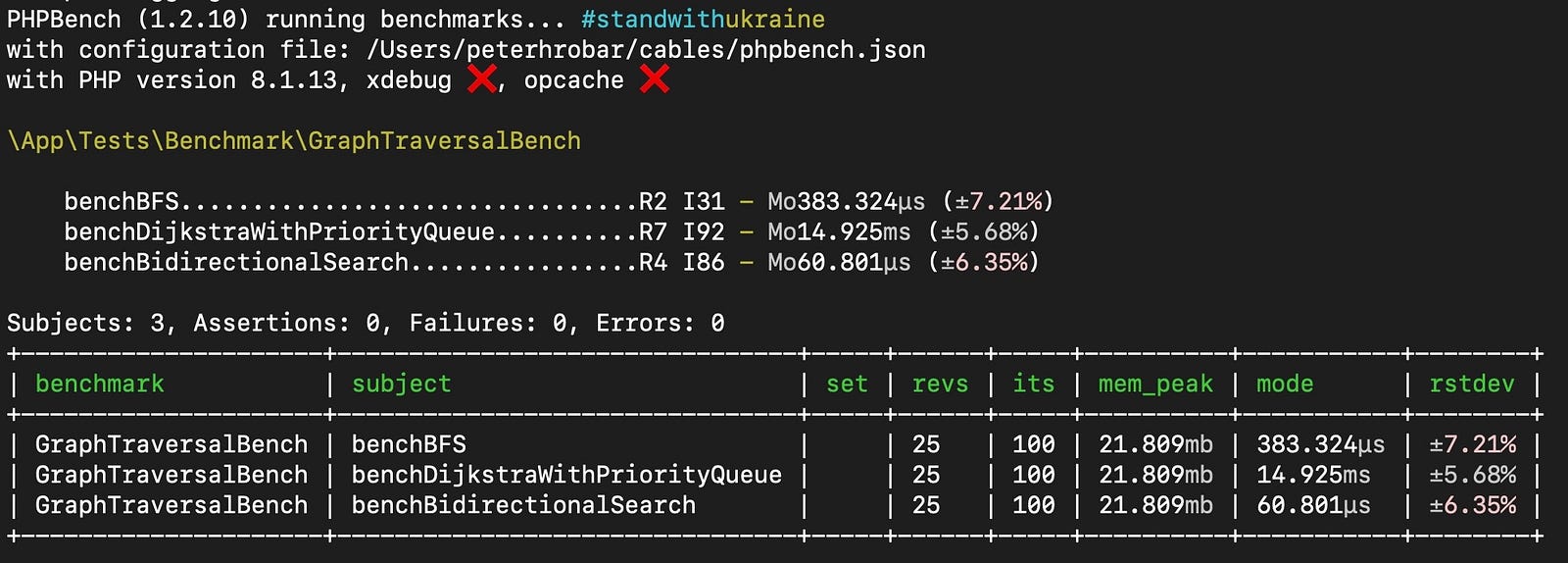
Benchmarking results for various path finding algorithms
The final results are not surprising.
The bidirectional search algorithm is a basically doing a BFS from the start and the end nodes respectively so this should be the quickest amongst the tested ones.
BFS is also very quick since we know the start and the end nodes (during testing it was using a non-weighted version of our graph).
Dijkstra’s algorithm on the other hand is much slower than the other two even with a priority queue based implementation.
This is due to the fact that it not only finds the path between the two given nodes but it also take into consideration the weight of the edges connecting them.
Since I was happy with it’s performance I decided to keep the original version of my BFS code.
With the given results I can easily translate the performance implications of switching to an other algorithm that can provide the advantages of using a weighted graph as well.